ในทางคณิตศาสตร์ "ฟังก์ชัน"
บัญญัติขึ้นโดย ไลบ์นิซ ใน พ.ศ. 2237 เพื่ออธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้ง
หรือจุดบนเส้นโค้ง
ฟังก์ชันที่ไลบ์นิซพิจารณานั้นในปัจจุบันเรียกว่า ฟังก์ชันที่หาอนุพันธ์ได้
และเป็นชนิดของฟังก์ชันที่มักจะแก้ด้วยผู้ที่ไม่ใช่นักคณิตศาสตร์
สำหรับฟังก์ชันชนิดนี้ เราสามารถพูดถึงลิมิตและอนุพันธ์ ซึ่งเป็นการทฤษฎีเซต พวกเขาได้พยายามนิยามวัตถุทางคณิตศาสตร์ทั้งหมดด้วย เซต ดีริคเลท และ โลบาเชฟสกี ได้ให้นิยามสมัยใหม่ของฟังก์ชันออกมาเกือบพร้อมๆกัน อ่านเพิ่มเติม
วันเสาร์ที่ 23 มกราคม พ.ศ. 2559
เลขยกกำลัง
เลขยกกำลัง
ใช้พื้นฐานเรื่องการคูณกันของจำนวน แล้วนำมาเขียนให้อยู่ในรูปเลขยกกำลัง
ในบทนี้จะได้เรียนเรื่องเลขยกกำลัง การบวกลบคูณและหารเลขยกกำลัง สูตรต่างๆ
ของเลขยกกำลัง การถอดรากที่ n ในระบบจำนวนจริง
การหารากที่สองของจำนวนอตรรกยะ และการแก้สมการที่ติดเครื่องหมายราก
เรื่องเลขยกกำลังเป็นพื้นฐานสำคัญของเรื่อง เอกซ์โพเนนเชียล และ ลอการิทึม อ่านเพิ่มเติม
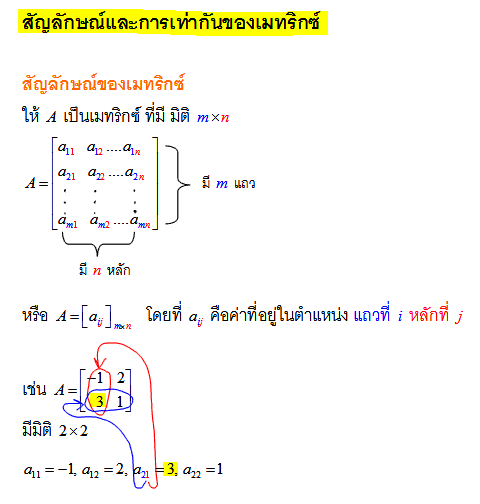
เมทริก
เราสามารถใช้เมทริกซ์แทนระบบสมการเชิงเส้น การแปลงเชิงเส้น และใช้เก็บข้อมูลที่ขึ้นกับตัวแปรต้นสองตัว เราสามารถบวก คูณ
และแยกเมทริกซ์ออกเป็นผลคูณของเมทริกซ์ได้หลายรูปแบบ เมทริกซ์เป็นแนวความคิดที่มีความสำคัญยิ่งของพีชคณิตเชิงเส้น โดยทฤษฎีเมทริกซ์เป็นสาขาหนึ่งของพีชคณิตเชิงเส้นที่เน้นการศึกษาเมทริกซ์
ในบทความนี้ แต่ละช่องของเมทริกซ์จะบรรจุจำนวนจริงหรือจำนวนเชิงซ้อน หากไม่ได้ระบุเป็นอย่างอื่น
ในบทความนี้ แต่ละช่องของเมทริกซ์จะบรรจุจำนวนจริงหรือจำนวนเชิงซ้อน หากไม่ได้ระบุเป็นอย่างอื่น
อ่านเพิ่มเติม
สมัครสมาชิก:
ความคิดเห็น (Atom)